Ángulos y rectas
Ángulos entre rectas
Relaciones entre parejas de ángulos
En casi todas las figuras geométricas donde intervengan rectas aparecen ángulos, los cuales es posible relacionar en cuanto a sus dimensiones y a su posición en el plano.
Así, dos ángulos pueden ser entre sí complementarios, suplementarios o adyacentes.
Dos ángulos son complementarios si la suma de sus medidas es 90°
α + β son complementarios
α + β= 90°
Dos ángulos son suplementarios si la suma de sus medidas es 180°
α + β son suplementarios
α + β = 180°
Geometría
La geometría es una parte de la matemáticas que se encarga de estudiar las propiedades y las medidas de una figura en un plano o en un espacio. Para representar distintos aspectos de la realidad, la geometría apela a los denominados sistemas formales o axiomáticos (compuestos por símbolos que se unen respetando reglas y que forman cadenas, las cuales también pueden vincularse entre sí) y a nociones como rectas, curvas y puntos, entre otras.
Angulo
La noción de ángulo, que procede del vocablo latino angŭlus, hace referencia a una figura de la geometría que se forma a partir de dos rectas que se cortan entre sí en una misma superficie. También puede decirse que un ángulo está formado por dos semirrectas que comparten un mismo vértice.
Los ángulos pueden medirse en diferentes unidades: el grado sexagesimal y el radiánson las medidas más frecuentes. De acuerdo a esta medición, los ángulos se clasifican de distintas maneras.
Si nos situamos en el terreno de los grados sexagesimales, un ángulo recto, por ejemplo, mide 90°. Si el ángulo mide menos de 90° pero más de 0°, se lo califica como agudo. En cambio, si mide más de 90° y menos de 180°, recibe el nombre de ángulo obtuso.
Si nos situamos en el terreno de los grados sexagesimales, un ángulo recto, por ejemplo, mide 90°. Si el ángulo mide menos de 90° pero más de 0°, se lo califica como agudo. En cambio, si mide más de 90° y menos de 180°, recibe el nombre de ángulo obtuso.
Segmento recta y una recta
Un segmento, en geometría, es un fragmento de recta que está comprendido entre dos puntos, llamados puntos extremos o finales. Así, dado dos puntos A y B, se le llama segmento AB a la intersección de la semirrecta de origen A que contiene al punto B con la semirrecta de origen B que contiene al punto A.
Recta: es una línea continua que esta formada por infinitos puntos en la misma direccion, la recta no tiene inicio ni fin
Semirrecta: es parte de una recta. En una recta si ubicamos un punto, esta delimitara dos semirrectas
se caracteriza por que tiene un inicio pero no un final.
Segmento de recta: si tomamos 2 puntos en una recta (T y S), el segmento de recta sera el conjunto de puntos comprendidos entre T y S.
se caracteriza por que :
Es una porcion o parte de una recta.
es la menor distancia posible entre dos puntos.
y por que tiene un principio y un final, por ende es suceptible de ser medido.
Segmentos consecutivos colineales: son los que tienen un extremo en comun, y si pertenecen a la misma recta
Segmentos consecutivos no colineales: son los que tienen un extremo en comun, pero, no pertenecen a la misma recta. (un ejemplo se puede ver en estos vectores)
.
Propiedad de la suma de segmentos: cumple con la propiedad asociativa y conmutativa.
Suma de Segmentos: para sumar dos o más segmentos hay que llevar sobre una recta y unirlos por un extremo. El resultado de la suma es la longitud que se obtenga.
Diferencia de segmentos: Para restar dos segmentos hay que superponerla para que coincidan en un extremo. La parte que sobra del mayor segmento es el resultado.
Mediatriz de un segmento: Es una recta perpendicular al segmento que pasa por su punto medio y lo divide en dos partes iguales.
Segmentos Concatenados: Son segmentos que tienen un punto en común, pero pertenecen a distintas rectas.
Semirrecta: es parte de una recta. En una recta si ubicamos un punto, esta delimitara dos semirrectas
se caracteriza por que tiene un inicio pero no un final.
Segmento de recta: si tomamos 2 puntos en una recta (T y S), el segmento de recta sera el conjunto de puntos comprendidos entre T y S.
se caracteriza por que :
Es una porcion o parte de una recta.
es la menor distancia posible entre dos puntos.
y por que tiene un principio y un final, por ende es suceptible de ser medido.
Segmentos consecutivos colineales: son los que tienen un extremo en comun, y si pertenecen a la misma recta
Segmentos consecutivos no colineales: son los que tienen un extremo en comun, pero, no pertenecen a la misma recta. (un ejemplo se puede ver en estos vectores)
.
Es una porcion o parte de una recta.
es la menor distancia posible entre dos puntos.
y por que tiene un principio y un final, por ende es suceptible de ser medido.
Segmentos consecutivos colineales: son los que tienen un extremo en comun, y si pertenecen a la misma recta
Segmentos consecutivos no colineales: son los que tienen un extremo en comun, pero, no pertenecen a la misma recta. (un ejemplo se puede ver en estos vectores)
.
Propiedad de la suma de segmentos: cumple con la propiedad asociativa y conmutativa.
Suma de Segmentos: para sumar dos o más segmentos hay que llevar sobre una recta y unirlos por un extremo. El resultado de la suma es la longitud que se obtenga.
Diferencia de segmentos: Para restar dos segmentos hay que superponerla para que coincidan en un extremo. La parte que sobra del mayor segmento es el resultado.
Mediatriz de un segmento: Es una recta perpendicular al segmento que pasa por su punto medio y lo divide en dos partes iguales.
Segmentos Concatenados: Son segmentos que tienen un punto en común, pero pertenecen a distintas rectas.
Suma de Segmentos: para sumar dos o más segmentos hay que llevar sobre una recta y unirlos por un extremo. El resultado de la suma es la longitud que se obtenga.
Diferencia de segmentos: Para restar dos segmentos hay que superponerla para que coincidan en un extremo. La parte que sobra del mayor segmento es el resultado.
Mediatriz de un segmento: Es una recta perpendicular al segmento que pasa por su punto medio y lo divide en dos partes iguales.
Segmentos Concatenados: Son segmentos que tienen un punto en común, pero pertenecen a distintas rectas.
Lineas paralelas
Las son dos o más líneas que nunca se intersectan. Hay ejemplos de líneas paralelas a nuestro alrededor, en los dos lados de ésta página y en los estantes de un librero. Cuando ves líneas paralelas o estructuras que aparentan seguir la misma dirección, nunca se cruzan unas a otras, y la distancia entre ellas es constante, es muy probable que sean líneas paralelas.
Las son dos o más líneas que nunca se intersectan. Hay ejemplos de líneas paralelas a nuestro alrededor, en los dos lados de ésta página y en los estantes de un librero. Cuando ves líneas paralelas o estructuras que aparentan seguir la misma dirección, nunca se cruzan unas a otras, y la distancia entre ellas es constante, es muy probable que sean líneas paralelas.
Lineas perpendiculares
Las líneas perpendiculares están en todos lados, no sólo en una gráfica en papel sino en el mundo que nos rodea, desde las intersecciones de las calles a las líneas de colores en una camisa a cuadros. En nuestra vida diaria, nos contentamos con llamar perpendiculares a esas líneas si aparentan estar en ángulo recto entre ellas. En el álgebra, usamos ecuaciones para asegurarnos de que realmente lo son.
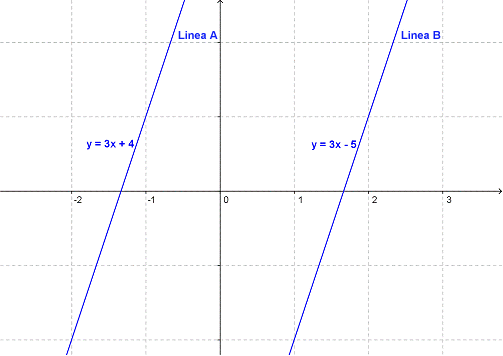
Comparemos las ecuaciones de líneas que son perpendiculares y de las que no lo son para ver si existe un patrón que nos permita reconocer a las líneas perpendiculares. Empezaremos con dos líneas que sabemos no lo son.
Las líneas perpendiculares están en todos lados, no sólo en una gráfica en papel sino en el mundo que nos rodea, desde las intersecciones de las calles a las líneas de colores en una camisa a cuadros. En nuestra vida diaria, nos contentamos con llamar perpendiculares a esas líneas si aparentan estar en ángulo recto entre ellas. En el álgebra, usamos ecuaciones para asegurarnos de que realmente lo son.
Comparemos las ecuaciones de líneas que son perpendiculares y de las que no lo son para ver si existe un patrón que nos permita reconocer a las líneas perpendiculares. Empezaremos con dos líneas que sabemos no lo son.
Clasificación de ángulos según su medida
1. Clasificación de ángulos según su medida Agudo < 90° Recto = 90° Obtuso>90° Convexo < 180° Llano = 180° Cóncavo > 180° Nulo = 0º Completo = 360° Negativo < 0º Mayor de 360°Tipos de ángulos según su posición Ángulos consecutivos Ángulos consecutivos son aquellos que tienen el vértice y un lado común.
1. Clasificación de ángulos según su medida Agudo < 90° Recto = 90° Obtuso>90° Convexo < 180° Llano = 180° Cóncavo > 180° Nulo = 0º Completo = 360° Negativo < 0º Mayor de 360°Tipos de ángulos según su posición Ángulos consecutivos Ángulos consecutivos son aquellos que tienen el vértice y un lado común.
Ángulos en rectas con ecuaciones
Ángulos opuestos por el vértice
Se denominan Ángulos opuestos por el vértice cuando los lados de uno son semi rectas contrarias a los lados del otro. Los ángulos opuestos al vértice tienen como propiedad que “todos los ángulos opuestos por el vértice son iguales”.
Esta propiedad es una de las más sencillas en el área de la geometría, se puede emplear al momento en que dos rectas se cruzan. Si un par de rectas se cruzan, va a formar 4 ángulos menores a 180º. Los 4 ángulos van a tener un punto en común el cual se denomina vértice, en este punto es donde se cortan las dos rectas. Si las rectas son perpendiculares entre ellas, los cuatro ángulos serán rectos, si las rectas no son perpendiculares, entonces dos de los ángulos serán agudos y los otros dos serán obtusos.
Cada Angulo agudo tendrá en común el vértice y un lado con cada uno de los ángulos obtusos; así mismo, un ángulo obtuso tendrá en común el vértice y un lado con cada ángulo agudo; igualmente, un ángulo agudo y uno obtuso deben sumar 180º debido a que presentan un lado en común y los otros lados pertenecen a una misma recta.
El Teorema de los ángulos opuestos por el vértice contempla el siguiente enunciado: Esta clase de ángulos son coherentes y precisos. Hipótesis: Alfa y Beta opuestos por el vértice. Tesis: Alfa es igual a Beta. Demostración: Alfa mas Y es igual a 180º por ser adyacentes; a su vez, Beta mas Y es igual a 180º por ser también adyacentes. Como consecuencia de la propiedad transitiva, los términos iniciales deben ser semejantes entre sí, es decir, Alfa más Y es igual a Beta más Y. por lo tanto Y es igual a sí mismo, sustrayéndolo en ambos miembros de la igualdad. Como conclusión se puede decir que las bisectrices de dos ángulos opuestos por el vértice son semirrectas opuestas.
Se denominan Ángulos opuestos por el vértice cuando los lados de uno son semi rectas contrarias a los lados del otro. Los ángulos opuestos al vértice tienen como propiedad que “todos los ángulos opuestos por el vértice son iguales”.
Esta propiedad es una de las más sencillas en el área de la geometría, se puede emplear al momento en que dos rectas se cruzan. Si un par de rectas se cruzan, va a formar 4 ángulos menores a 180º. Los 4 ángulos van a tener un punto en común el cual se denomina vértice, en este punto es donde se cortan las dos rectas. Si las rectas son perpendiculares entre ellas, los cuatro ángulos serán rectos, si las rectas no son perpendiculares, entonces dos de los ángulos serán agudos y los otros dos serán obtusos.
Cada Angulo agudo tendrá en común el vértice y un lado con cada uno de los ángulos obtusos; así mismo, un ángulo obtuso tendrá en común el vértice y un lado con cada ángulo agudo; igualmente, un ángulo agudo y uno obtuso deben sumar 180º debido a que presentan un lado en común y los otros lados pertenecen a una misma recta.
El Teorema de los ángulos opuestos por el vértice contempla el siguiente enunciado: Esta clase de ángulos son coherentes y precisos. Hipótesis: Alfa y Beta opuestos por el vértice. Tesis: Alfa es igual a Beta. Demostración: Alfa mas Y es igual a 180º por ser adyacentes; a su vez, Beta mas Y es igual a 180º por ser también adyacentes. Como consecuencia de la propiedad transitiva, los términos iniciales deben ser semejantes entre sí, es decir, Alfa más Y es igual a Beta más Y. por lo tanto Y es igual a sí mismo, sustrayéndolo en ambos miembros de la igualdad. Como conclusión se puede decir que las bisectrices de dos ángulos opuestos por el vértice son semirrectas opuestas.
Ángulos entre paralelas y una secante
Al cortar dos rectas con una secante se forman ocho ángulos, los cuales se representan por letras minúsculas; éstos se clasifican por parejas de acuerdo con la posición que tienen con la secante. Ángulos colaterales internos: son los ángulos que se encuentran del mismo lado de la secante y dentro de las rectas.
Al cortar dos rectas con una secante se forman ocho ángulos, los cuales se representan por letras minúsculas; éstos se clasifican por parejas de acuerdo con la posición que tienen con la secante. Ángulos colaterales internos: son los ángulos que se encuentran del mismo lado de la secante y dentro de las rectas.
Ángulos entre lineas paralelas
Una recta que corta a otras dos rectas paralelas hace los ángulos alternos iguales, los ángulos externos iguales a los interiores y opuestos, y la suma de los ángulos internos por el mismo lado iguales a dos rectos.
Una recta que corta a otras dos rectas paralelas hace los ángulos alternos iguales, los ángulos externos iguales a los interiores y opuestos, y la suma de los ángulos internos por el mismo lado iguales a dos rectos.
